Mit dem Beitrag „Statistische Logik“ geht unsere Reihe „Kennzahlen – die unbekannten Wesen“ zu Ende. Vielen Dank noch einmal an Herrn Prof. Schaffner, der die Kennzahlen für uns zu bekannten Wesen gemacht hat! Wie schon bei den letzten Artikeln, finden Sie eine Übersicht der Reihe am Ende des Artikels.
Kennzahlen basieren oft auf eindimensionalen Datenreihen (x1, x2, x3, … xn), die durch Mittelwerte gekennzeichnet werden. Beispiel: Aus 110 Dokumenten wird zufällig eine 10%-Stichprobe gezogen, deren Orthografiefehler gezählt und auf 1.000 Wörter normiert werden. Die Werte lauten: (1,2; 0,7; 1,6; 0,8; 0,9; 3,5; 1,7; 0,9; 1,1; 1,3; 0,75). Aufgrund eines sehr fehlerhaften Dokuments (orthQuote: 3,5 beim sechsten Dokument), wäre der arithmetische Mittelwert (1,314) vielleicht keine geeignete Kennzahl, wenn dieser Ausreißer durch eine untypische Situation hervorgerufen wurde (z.B. Schüler-Praktikant). Die Datenreihe könnte getrimmt werden (Vernachlässigung der Ausreißer). Der getrimmte Mittelwert ist 1,095 (der Ausreißer „3,5“ wird aus der Berechnung des arithmetischen Mittels entfernt). Es könnte aber auch der Median (1,1) als Maßzahl gewählt werden. Dabei wird die Datenreihe zunächst nach Größe sortiert, wobei der 6. Wert (1,1) die sortierte Datenreihe halbiert. Der Modalwert (0,9) wäre vermutlich keine geeignete Maßzahl, da der häufigste Wert kein plausibles Ergebnis liefert.
Arithmetisches Mittel
Der empirische Mittelwert ist die Summe aller Merkmalsausprägungen, geteilt durch die Größe der Stichprobe. Beim „getrimmten“ arithmetischen Mittel werden die Ausreißer aus der Datenreihe entfermt.
Median
Dies ist der Wert, der die Datenreihe in zwei Hälften teilt (ggfs. bei einer geradzahligen Datenreihe errechnet). Dazu werden die Werte zunächst nach ihrer Größe sortiert. Der Median ist unempfindlicher gegen Ausreißer als der Mittelwert.
Modalwert (Modus)
Der Modus ist der am häufigsten auftretende Wert einer Datenreihe. Er ist auch der einzige Mittelwert, der bereits bei einer Nominalskala (unterscheidbare Ausprägungen ohne natürliche Rangfolge, z.B. Postleitzahlen, Berufsgruppen, Kundennamen, Fehlerklassen) angewendet werden kann.
Der Lageparameter reicht aber oft nicht aus, um die Merkmale einer Datenreihe befriedigend zu beschreiben. So interessiert beim arithmetischen Mittelwert beispielsweise, wie weit die einzelnen Werte von diesem Lageparameter entfernt liegen – wie variabel sie sind. Zur Untersuchung dient das Streuungsmaß.
Die Streuung gibt die Verteilung von einzelnen Werten um den Mittelwert herum an. Beispielsweise haben die Datenreihe a = (10, 50, 100) und b = (49, 50, 51) den gleichen Mittelwert (x=50) , streuen aber unterschiedlich. Bei der Datenreihe a liegt eine starke Streuung, bei b eine schwache Streuung vor. Einer der wichtigsten Streuungsparameter ist die Varianz (s2). Bei der Datenreihe a beträgt die Varianz 1,367(Rechnung: (402+02+502)/3) bei der Datenreihe b beträgt die Varianz nur 0,666 (Rechnung: (12+02+12)/3).
Die Varianz ist ein wichtiges Streuungsmaß, das als mittlere quadratische Abweichung der einzelnen Messwerte xi vom arithmetischen Mittelwert x berechnet wird.
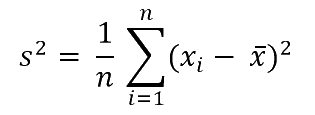
Die Standardabweichung s wird als positive Wurzel der Varianz s2 errechnet. Je geringer die Varianz bzw. Standardabweichung ausfallen, umso geringer ist die Streuung – die Daten weisen wenig Variabilität aus. Sind alle Werte einer Datenreihe identisch, sind Varianz und Standardabweichung gleich null.[i]
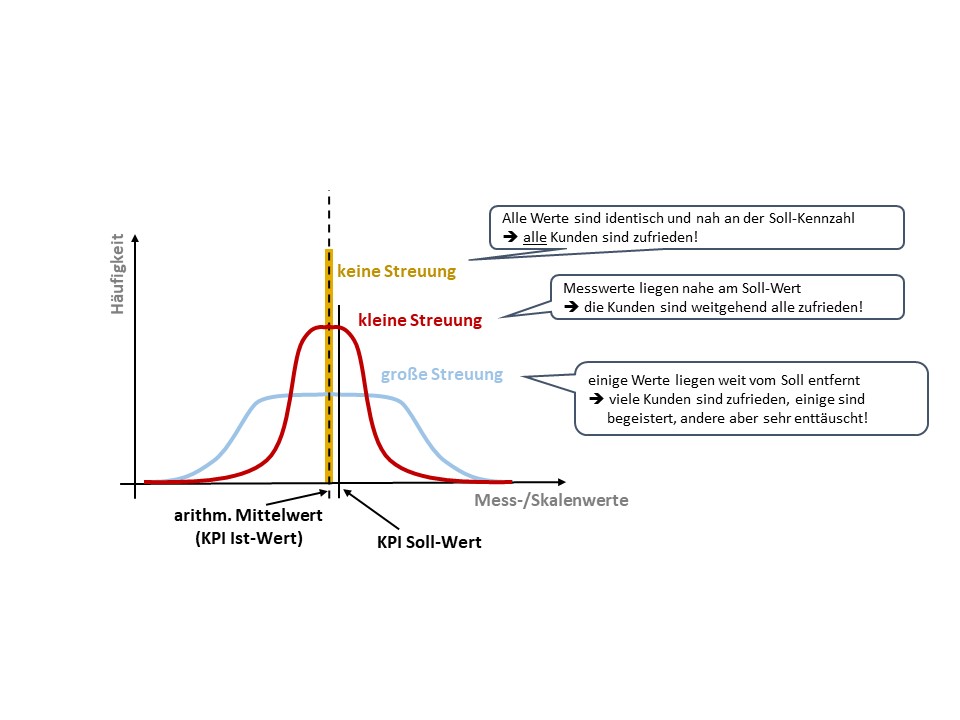
Die Streuung der Grunddaten ist oft wichtiger als die Kennzahl selbst. Bei der Interpretation einer Kennzahl darf also nicht nur interessieren, wie nah z.B. eine Qualitätskennzahl (Ist) an der Vorgabe (Soll) liegt, sondern wie sich die Streuung der Einzelwerte darstellt. Ist die Streuung einer Datenreihe für Orthografiefehler in Dokumenten groß (in der 11er Datenreihe wäre s2=0,58 ), wird es vermutlich viele zufriedene Kunden und einige begeisterte, aber auch einige enttäuschte Kunden geben. Dies könnte zu Reklamationen führen. Und sind die „falschen“ Kunden unzufrieden, führt dies ausgerechnet zum Verlust der A- und B-Kunden. Ist die Streuung dagegen gering (Beispiel: die elf Werte würden rund um 1,3 streuen), hätten wir mit einer Varianz nah an Null eine ausgewogene Kundenzufriedenheit. Wäre 1,3 auch der Soll-Wert (Vorgabe) unserer Kennzahl, wäre auch eine mutmaßlich angemessen hohe Kundenzufriedenheit zu vermuten (Vgl. Abb. 6). [ii]
Korrelation ist nicht gleich Kausalität
Maßzahlen können zudem in einer gemeinsamen Entwicklung zueinanderstehen, sich miteinander oder gegeneinander entwickeln (Korrelation). Wenn sich ein Merkmal y in strenger Abhängigkeit zu einem anderen (unabhängigen) Merkmal x entwickelt, wird von einem Ursache-Wirkungs-Zusammenhang (Kausalität) gesprochen (x ⇒ y). Dies kann quantitativ über zwei Datenreihen, (x1, x2, x3, … xn) und (y1, y2, y3, … yn), abgebildet werden (z.B. Dokumentgröße zu Orthografiefehlern). Es sind aber auch qualitative Zusammenhänge denkbar.
Grundsätzlich besteht ein großer Unterschied zwischen einem reinen Zusammenhang zwischen zwei Variablen x und y (Korrelation) und einer tatsächlichen Auswirkung von einer Variable x auf die Variable y (Kausalität). Denn ist eine Korrelation zwischen zwei Variablen erkennbar, kann dies auf vier mögliche Ursachen zurückgeführt werden. Die nachfolgend dargestellten Phänomene gelten für quantitative wie qualitative Daten, bei den Beispielen wird sich jedoch auf nicht-numerische Daten konzentriert.
- Es besteht ein tatsächlicher Wirkungszusammenhang von x auf y (Kausalität).
Dieser muss aber nicht monokausal sein. So könnte gegebenenfalls zusätzlich eine dritte Variable z auf y einwirken (x ⇒ y und z ⇒ y).
Beispiel: Die Einhaltung von Terminologie „x“ wirkt auf die redaktionelle Textqualität „y“. Zusätzlich wirkt aber auch die sprachliche Ausdrucksfähigkeit des Redakteurs „z“ auf „y“. - Es besteht ein sogenannter beidseitiger Zusammenhang (x ⇒ y und y ⇒ x). Beispiel: Bekanntheitsgrad eines Produktes „x“ und dessen Verkaufszahlen „y“.
- Es existiert ein indirekter Zusammenhang, bei der die Variable x nur über eine dritte, nicht betrachtete Variable z, auf die Variable y wirkt. Beispiel: Die Einführung eines Redaktionssystems „x“ wirkt nicht unmittelbar auf die Zufriedenheit der Kunden mit der Produktliteratur „y“. Da aber die redaktionelle Qualität „z“ verbessert wird, ist ein Zusammenhang feststellbar.
- Es handelt sich um einen rein zufälligen Effekt (Scheinkorrelation).
Beispiel: Erneuerung der Arbeitsplatzbeleuchtung „x“ und Verbesserung der Textqualität „y“.
Es ist höchst gefährlich, eine mögliche Korrelation ohne tiefergehende Analysen kausal zu interpretieren und aus einem vermeintlichen Zusammenhang eine eindeutige Ursachen-Wirkungs-Beziehung abzuleiten.
In der Korrelationsrechnung werden Zusammenhänge zweier metrisch skalierter Datenreihen untersucht (metrisch skaliert = gleichabständige Skalenwerte). Über die Kovarianz sxy wird, über die mittlere gemeinsame Abweichung der Daten von den Mittelwerten, ein grundsätzlicher Zusammenhang festgestellt. Ist die Kovarianz gleich null, gelten die Merkmale als unkorreliert.
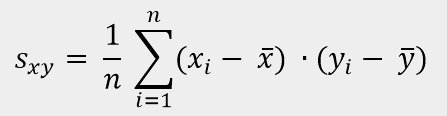 Der Korrelationskoeffizient rxy misst die Stärke eines linearen Zusammenhangs und ist definiert (nach Bravais-Pearson) als Quotient aus der Kovarianz und dem Produkt der Standardabweichungen.
Der Korrelationskoeffizient rxy misst die Stärke eines linearen Zusammenhangs und ist definiert (nach Bravais-Pearson) als Quotient aus der Kovarianz und dem Produkt der Standardabweichungen.
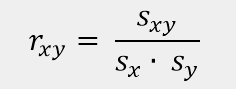 Die Regressionsrechnung dient schließlich dazu, eine geeignete funktionale Beziehung zwischen x und y zu modelieren (z.B. Gerade, Parabel), um die Kausalität zu begründen. Der Signifikanztest untersucht, ob die Befunde der Stichprobe auf die Grundgesamtheit übertragen werden können (z.B. mittels t-Test).[iii]
Die Regressionsrechnung dient schließlich dazu, eine geeignete funktionale Beziehung zwischen x und y zu modelieren (z.B. Gerade, Parabel), um die Kausalität zu begründen. Der Signifikanztest untersucht, ob die Befunde der Stichprobe auf die Grundgesamtheit übertragen werden können (z.B. mittels t-Test).[iii]
Bei qualitativen Phänomen bietet sich – unter strenger Beachtung der qualitativen Gütekriterien – das logische Schließen an, um Paradoxien auszuschließen. Beim induktiven Vorgehen wird von Beobachtungen ausgehend auf eine mögliche Gesetzmäßigkeit geschlossen. Deduktiv werden spezifische Aussagen aus einer allgemeinen Gesetzmäßigkeit abgeleitet (aus Prämissen folgen Konklusionen). Hilfreich dabei sind multiperspektive Diskussionen (Wahrung weitgehender Objektivität) sowie dialektische Argumentationen (zu jeder These eine Antithese formulieren).
Bei quantitativen Phänomenen (Datenreihen) wird die Korrelationsrechnung angewendet. Hier dient die Kovarianz s zur Bestimmung eines grundsätzlichen Zusammenhangs (z.B. Dokumentgröße und Fehlerquote) und der Korrelationskoeffizient r zur Bestimmung der Richtung und Stärke. Bei einem linearen Zusammenhang zwischen zwei betrachteten Merkmalen x und y kann r zwischen „-1“ und „+1“ liegen. Er stellt damit den positiven (bzw. negativen) Linearzusammenhang dar, bei r = 0 wären beide Merkmale linear unabhängig.
Schlussbetrachtung
Dass in der Praxis vielfach von einer Dominanz der Kennzahlen berichtet wird, kann auf mehrere Ursachen zurückgeführt werden – beispielsweise eine zu starke Kennzahlen-Gläubigkeit, eine unangemessene Anzahl oder Ausrichtung von Kennzahlen oder rein top-down gesteuerte Kennzahlen. Zu empfehlen ist, dass sich Funktionsträger in Fachabteilungen aktiv engagieren und gemäß des Konzepts „Ursachen-Controlling“ Gedanken über die Einflussfaktoren auf die Zielerreichung konzentrieren („schwache“ Signale). Dies wird in aller Regel vom Management positiv geschätzt und der Druck von Oben sinkt. Gleichzeitig sollte die Erstellung eines Kennzahlenkonzept systematisch erfolgen, woraus sich auch zwingend Vorgaben für Metadaten ergeben, sowie mit einem Grundverständnis für Statistik.
Fußnoten:
[i] Zur Vertiefung: Schuldenzucker, U.: Prüfungstraining – Deskriptive Statistik, Stuttgart: Schäffer-Poeschel, S. 42 ff
[ii] Schaffner, M. (2018): „Vom Wiegen wird die Sau nicht fett!“ Oder: das Kennzahlen-Paradoxon, in: tcworld GmbH (Hrsg.), Proceedings tekom-Frühjahrstagung 2018, S. 96-101, tcworld GmbH, Stuttgart
[iii] Zur Vertiefung: Schuldenzucker, U.: Prüfungstraining – Deskriptive Statistik, Stuttgart: Schäffer-Poeschel, S. 85 ff
Übersicht Beiträge Kennzahlen:
- Schlüssiges Vorgehen (Teil 1)
- Strategische Früherkennung (Teil 2)
- Empirische Arbeit (Teil 3)
- Statistische Logik (Teil 4)